题目快照

题目描述

给定 n 个二维欧几里得平面上的点 p1, p2, ……, pn，请输出距离最近的两个点的距离。

输入格式

输入第一行为一个正整数 n，表示点数。

接下来 n 行，第 i 行为用空格隔开的整数 xi, yi，表示 pi = (xi, yi)。

输入保证：没有两个坐标完全相同的点。

输出格式

输出一行，包含一个整数 $D^2$，表示距离最近的两个点的距离的平方 。

由于输入的点为整点，因此这个值一定是整数。

解题思路

这道题是分治的模版题之一，其实求的就是求的是在给定的点集 中，距离最近的两个点的距离的平方。
在题目的下方有些时间复杂度要求为 n log^2 n 所以肯定是不能暴力的啦
既然是要求一个平面内最近的点对，那这个平面是不是可以无线分割，一直到只有俩个点
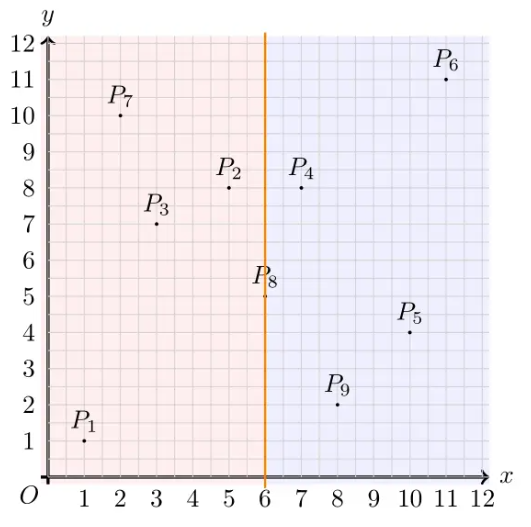
所以我们可以把它分一半平面内的最近点对距离 min1和另一半平面内的最近点对距离 min2 。此时更新 ans = min(min1, min2)

计算出俩个平面内的最近点对后，还要继续考虑俩个平面间的最近点对。
又因为我们已经计算出俩个平面内的最近点对距离了，所以为了减少计算量，俩个平面间点的距离就不应该超过先前计算出的值，我们可以以 点到中线的横轴距离X小于ans 与 俩个点的纵轴距离Y小于ans 来筛选出一些不必要计算的点。
不断递归，最后就能计算出我们要的值。

AC Code

#include <bits/stdc++.h>
#define INF 0x7f7f7f7f
using namespace std;

long long n;
struct node
{
    double x, y;
}a[400010], c[400010];

bool cmp(node x, node y){
    return x.x < y.x;
}

bool cmpl(node x, node y){
    return x.y < y.y;
}

double dis(long long i, long long j){
    double dx = c[i].x - c[j].x, dy = c[i].y - c[j].y;
    return sqrt(dx * dx + dy * dy);
}

double slv(long long l, long long r){
    // 划分区域只剩下一个点 返回距离为无穷大
    if(l == r) return INF;

    // 分
    long long mid = (l + r) / 2;
    long long num = 0;
    double ans = min(slv(l, mid), slv(mid + 1, r));

    // 治
    // 如果点与中间线的X距离 大于 俩各区域内的距离最小值 该点根本没有计算的必要
    for(long long i = l; i <= r; i++){
        if(abs(a[mid].x - a[i].x) <= ans) c[++num] = a[i];
    }

    // 按照 Y轴 大小排序 从小到大
    sort(c + 1, c + num + 1, cmpl);

    // 分别计算筛选后的点的距离 如果俩个点的纵轴距离超过当前俩各区域内的距离最小值 那也没必要计算 又因为是按照大小排序的 所以可以直接跳出循环 计算下一个点
    for(long long i = 1; i <= num; i++)
        for(long long j = i + 1; j <= num; j++){
            if(c[j].y - c[i].y >= ans) break;
            ans = min(ans, dis(i, j));
        }
    return ans;
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> n;

    // 录入点集
    for(long long i = 1; i <= n; i++){
        cin >> a[i].x >> a[i].y;
    }

    //按照 X轴 排序 从小到大
    sort(a + 1, a + n + 1, cmp);
    printf("%.0lf", pow(slv(1, n), 2));
    return 0;
}