题目快照

猫猫 TOM 和小老鼠 JERRY 最近又较量上了，但是毕竟都是成年人，他们已经不喜欢再玩那种你追我赶的游戏，现在他们喜欢玩统计。

最近，TOM 老猫查阅到一个人类称之为“逆序对”的东西，这东西是这样定义的：对于给定的一段正整数序列，逆序对就是序列中 ai > aj 且 i < j 的有序对。知道这概念后，他们就比赛谁先算出给定的一段正整数序列中逆序对的数目。注意序列中可能有重复数字。**

输入格式

第一行，一个数 n，表示序列中有 n 个数。

第二行 n 个数，表示给定的序列。序列中每个数字不超过 10^9

输出格式

输出序列中逆序对的数目。

解题思路与代码

这道题有仨个解法，最暴力的肯定是逐一对比（类似于冒泡排序 一个一个比较大小）。但是肯定是过不了的，所以下面记录俩个时间复杂度比较低的方法。

归并排序（分治法）

所谓分治，就是分而治之，将复杂的问题分成若干个相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。

采用分治法解决的问题一般具有的特征如下：

1. 问题的规模缩小到一定的规模就可以较容易地解决。
2. 问题可以分解为若干个规模较小的模式相同的子问题，即该问题具有最优子结构性质。
3. 合并问题分解出的子问题的解可以得到问题的解。
4. 问题所分解出的各个子问题之间是独立的，即子问题之间不存在公共的子问题。

这道题计算逆序数就可以分子问题分到直到俩俩比对——
拿一个例子来说
过程① —— 分
5 4 2 6 3 1
5 4 2 | 6 3 1
5 4 | 2 | 6 3 | 1
过程② —— 治

第一轮

5 4
i j k
此时mid = 1
i > j 4 _

此时 ans += mid - i + 1 = 0 + 1 - 1 + 1 = 1

第二轮

4 5 2 _
i j k
此时的 mid = 2
i > j 2
ans += mid - i + 1 = 1 + 2 - 1 + 1 = 3

剩下的省略了 过程一致……

即在归并排序时，若发现有前面的数（a[i]）大于后面的数（a[j]）时,发现逆序对。此时a[l]~a[m]为有序数列。此时有（mid-i+1）个逆序对。则在遇到这种情况时将结果加上（m-i+1）个即可。

代码如下：

#include <bits/stdc++.h>
using namespace std;
int n, a[500010], c[500010];
long long ans;

void msort(int b, int e){
    // 分

    if(b == e) return;
    int mid = (b + e) / 2, i = b, j = mid + 1, k = b;
    msort(b, mid);
    msort(mid + 1, e);

    // 治
    while(i <= mid && j <= e){
        if(a[i] <= a[j]) c[k++] = a[i++];
        else c[k++] = a[j++], ans += mid - i + 1;
        // 代码关键之处 ans的计数
    }

    while(i <= mid){
        c[k++] = a[i++];
    } 
  
    while(j <= e){
        c[k++] = a[j++];
    }

    for(int f = b; f <= e; f++){
        a[f] = c[f];
    }

}

int main(){
    cin >> n;
    for(int i = 1; i <= n; i++){
        cin >> a[i];
    }
    msort(1, n);
    cout << ans;
    return 0;
}

树状数组

树状数组(Binary Indexed Tree(B.I.T), Fenwick Tree)是一个查询和修改复杂度都为logn的数据结构。主要用于查询任意两位之间的所有元素之和，但是每次只能修改一个元素的值；经过简单修改可以在logn的复杂度下进行范围修改。
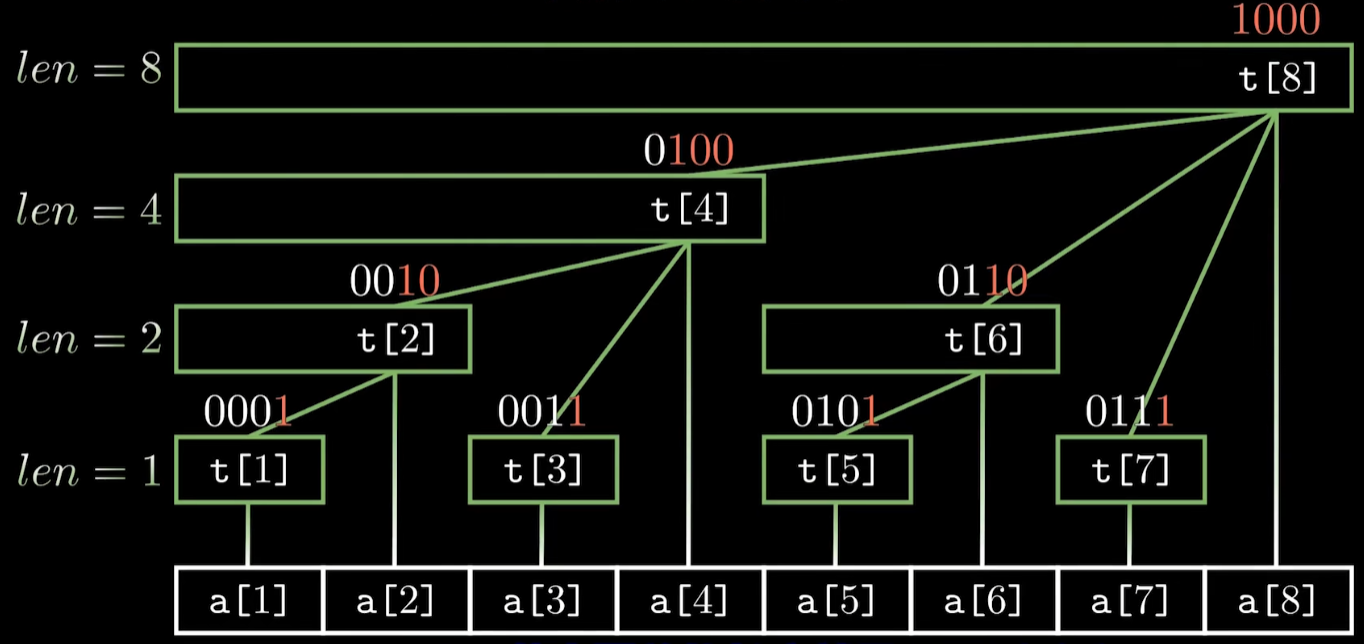
它的结构如下展示：

可见，比如要求A[1]~A[5]的和，只需要求 T[4] + T[5] 即可， 求前缀和非常的方便
在这题里，我们就可以用树状数组记录在第i个数之前按有几个数比它小或等于他，即ai <= aj 那么我们就要删除这些数。即用i−query(ranklist[i])即可。

但是数据可能出现非常大的数，例如1 2 99999999，对于树状数组来说第三个数明显太大，所以我们可以将数据离散化，所谓离散化在这也就只是排个序，然后再重新覆盖回去啦 例如 3 9 8 1，离散化后变成了 2 4 3 1，离散化后的数据大小关系并没有发生改变，所以他们的逆序数其实是一样的。

所以我们可以写出如下的代码。
（注意题目中的序列可能有重复数字，所以要所有与 ai 相等的元素中，先出现的也应该标记为较小）

#include <bits/stdc++.h>
using namespace std;

struct node
{
    int num, val;
}a[500010];
int n;
int ranklist[500010], tree[500010];
bool cmp(node a, node b) {
    if (a.val != b.val) {
        return a.val < b.val;
    } else {
        return a.num < b.num;
        // 先出现的标记为较小，这样就不会计入逆序数中了
    }
}
void insert(int i, int x){
    while(i <= n){
        tree[i] += x;
        i += i & (-i);
    }
}

int query(int x){
    int sum = 0;
    for(;x; x -= x & (-x)){
        sum += tree[x];
    }
    return sum;
}

int main(){

    cin >> n;
    for(int i = 1; i <= n; i++){
        cin >> a[i].val;
        a[i].num = i;
    }
    sort(a + 1, a + n + 1, cmp);
    for(int i = 1; i <= n; i++){
        ranklist[a[i].num] = i;
    }

    long long ans = 0;
    for(int i = 1; i <= n; i++){
        insert(ranklist[i], 1);
        ans += i - query(ranklist[i]);
    }
    cout << ans;
    return 0;
}